dnd, graphs
This year there is an RPG game jam for making zungeons, which are zine-inspired D&D dungeons. Marcia B’s Bite-Sized Dungeons is a good starting point.
Marcia created a list of ten abstract dungeon layouts. I found two other layouts that essentially “finish the collection”, and the graph theory behind it is fun to explore.
Criterion
In the language of graph theory, Marcia is recommending that the abstract dungeon layouts be connected, planar graphs with six vertices and six edges.
Possible layouts
Marcia’s post lists ten such layouts. She mentions that hexagons also meet her criterion, but that she isn’t interested in plain loops.
It turns out that there are exactly 13 such layouts. The two which do not appear on Marcia’s blog are:
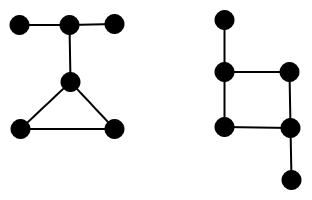
Rendered in Dungeonscrawl, these could look like:
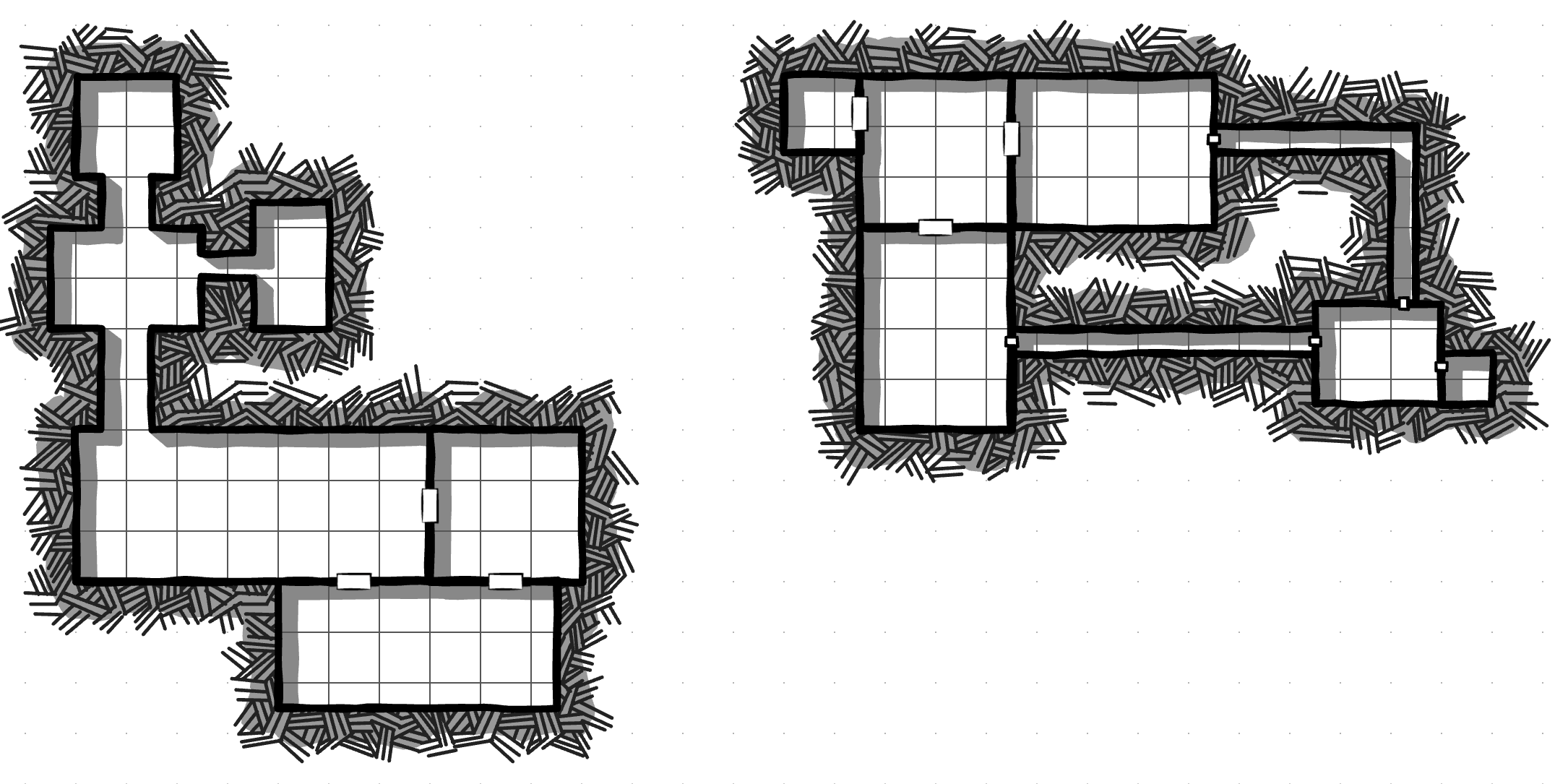
So if we throw out hexagons, we can randomly choose a layout with a d12.
By “exactly 13 layouts”, I mean up to graph-isomorphism. This may not, however, be a good assumption in practice. The following two graphs are graph-isomorphic, but are arguably different enough as dungeons:
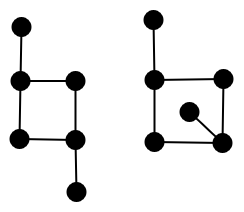
Resources for connected, planar graphs
The house of graphs contains a collection of connected, planar graphs in graph6 format.
If you download the collection of order 6 graphs, you can easily
find the ones with six edges using the
showg program.
The -e flag will display the number of edges:
$ showg planar_conn.6.g6 -eAny graph whose second line is
6 6will correspond to one of the abstract dungeon layouts. So you can count them with:
$ showg planar_conn.6.g6 -e | grep "^6 6$" | wc -lSeven-room dungeons?
Connected, planar graphs make good sense as an abstract layout for a dungeon. Six rooms/vertices was chosen as a sweet spot in game design. With six vertices, five edges is enough to connect the graph. The sixth edge gives the dungeon a loop.
Every connected, planar graph that has the same number of vertices as edges has exactly one loop. More generally, Euler’s formula says that:
\[ v - e + f = 2 \]
where
- v is the number of vertices
- e is the number of edges
- f is the number of faces
Note that one of the faces is always the outer, infinitely large region. Let’s refer to the finite faces as “regions”.
So if we want, say, a seven-room dungeon with two regions, we would choose eight edges.
How many layouts?
Using the data from the house of graphs:
| rooms | regions | total layouts |
|---|---|---|
| 6 | 1 | 13 |
| 7 | 1 | 33 |
| 7 | 2 | 67 |
| 8 | 1 | 89 |
| 8 | 2 | 236 |
| 8 | 3 | 486 |
| 9 | 1 | 240 |
| 9 | 2 | 797 |
| 9 | 3 | 2,075 |
| 9 | 4 | 4,454 |
| 10 | 1 | 657 |
| 10 | 2 | 2,678 |
| 10 | 3 | 8,548 |
| 10 | 4 | 22,768 |
| 10 | 5 | 51,816 |
| 11 | 1 | 1,806 |
| 11 | 2 | 8,833 |
| 11 | 3 | 33,851 |
| 11 | 4 | 109,072 |
| 11 | 5 | 302,451 |
| 11 | 6 | 714,987 |